
Have you seen my new found interest?
A hu hu.
Its back to POKEMON!!
Since black/white (dusk/dawn) is already out, I began to do a little bit of research.
First discovery of research.
N = <3 cheren=" Intellect" touko=" Actually">Lampure->Chandelure
Candle->Lamp->Chandelier.
Well I guess its not as bad as the starter pokemon... But I are still disappoint. D:<
Formally, a Menger sponge can be defined as follows:
where M0 is the unit cube and
Long story short: N is the 'king' of Team Plasma and they believe that Pokemon and Humans should be treated equally. (Communism?)
http://en.wikipedia.org/wiki/Enharmonic
In Pythagorean tuning, all pitches are generated from a series of justly tuned perfect fifths, each with a ratio of 3 to 2. If the first note in the series is an A♭, the twelfth note in the series, G♯, will be higher than the seventh octave (octave = ratio of 1 to 2, seven octaves is 1 to 27 = 128) of the A♭ by a small interval called a Pythagorean comma. This interval is expressed mathematically as:
Don't worry. My guess is as good as yours. So just sit back, relax, and just smile and nod. :D
P.s. N is the pretty one to the right with luscious green hair. >w<
Puppet.

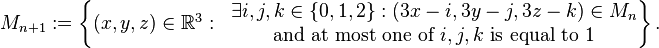
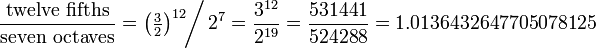
No comments:
Post a Comment